Chapter 3

Expansion and Factorisation of Quadratic Equations

What is expansion?

Expansion is removing of the brackets of an equation by solving the equation inside the brackets first.

Let me show you a simple example:

2+(10-5)

= 2+5

=7

What is factorisation?

Factorisation is the opposite process of expansion, which is finding the common factor(s) to get an expression.

Let me show you a simple example:

5x + 5

= 5(x+1)                      5 is the common factor of 5x and 5.

Difference between expansion and factorisation

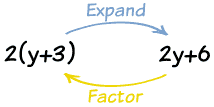
Expansion and factorisation is the opposite of one another. Expansion is to eliminate the brackets and to open up everything, while factorisation is to find the common factor and put it back into the brackets again.

Addition and Subtraction of Quadratic Expressions

x² = x X x

First off, let’s start with the simple addition and subtraction of quadratic equations

2x² + 4x² = 6x²

22x² – 10x² = 12x²

-4x-(-3x²) = =4x+3x²                   

*take note that x cannot be combined together because x and x^2 is two different terms.

Negative of a quadratic expression

For example:

-x+2 = -2-x 

This is because - is being multiplied to the both x and 2 inside the brackets.

Expansion and Simplification of Simple Quadratic Expressions

For example:

3(x+8) = 3x + 24

And another example:

and group the like terms together,

3a + 12 +4a +8 = 7a + 20

Expanding Quadratic Expressions of the form (a+b)(c+d)

For example, we have:

(3x+5)(2x+4) 

= 3x(2x+4) + 5(2x+4)

= 12x² + 12x + 10x + 20 For example:

= 12x² + 22x + 20

Another example:

Factorisation of Quadratic Expressions

For example:

x² + 5 + 6x = (x+1)(x+5)

we can form this table accordingly, and find the common factors of 5, and cross multiply both sides to form the right column. Add up the right column which will give the other term. The answer will be the equations on the left column, which is (x+1)(x+5).

This sums up the chapter!